Arbeitsblatt: Übungsblatt - Lineare Funktionen

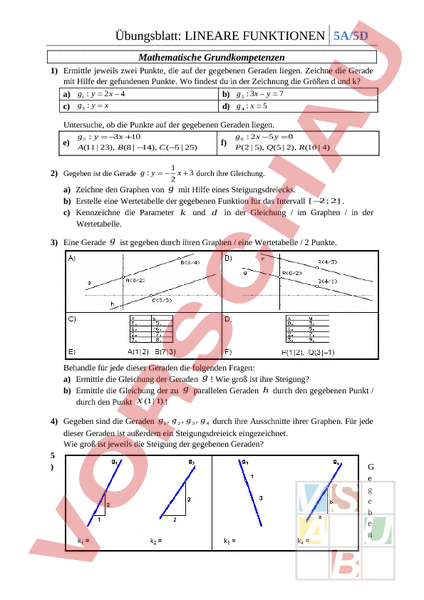
Übungsblatt: LINEARE FUNKTIONEN 5A/5D Mathematische Grundkompetenzen 1) Ermittle jeweils zwei Punkte, die auf der gegebenen Geraden liegen. Zeichne die Gerade mit Hilfe der gefundenen Punkte. Wo findest du in der Zeichnung die Größen und k? a) g1 y 2 4 b) 2 3x 7 c) 3 y x d) 4 x 5 Untersuche, ob die Punkte auf der gegebenen Geraden liegen. e) 5 y 3 10 A(11 23), (8 14), (5 25) f) 6 2 5 0 ( 2 5), (5 2), (10 4) 1 2 2) Gegeben ist die Gerade : 3 durch ihre Gleichung. a) Zeichne den Graphen von mit Hilfe eines Steigungsdreiecks. b) Erstelle eine Wertetabelle der gegebenen Funktion für das Intervall [2 2] c) Kennzeichne die Parameter und in der Gleichung im Graphen in der Wertetabelle. 3) Eine Gerade ist gegeben durch ihren Graphen eine Wertetabelle 2 Punkte. Behandle für jede dieser Geraden die folgenden Fragen: a) Ermittle die Gleichung der Geraden ! Wie groß ist ihre Steigung? b) Ermittle die Gleichung der zu parallelen Geraden durch den gegebenen Punkt durch den Punkt (1 1) 4) Gegeben sind die Geraden g1 g 2 g 3 g 4 durch ihre Ausschnitte ihrer Graphen. Für jede dieser Geraden ist außerdem ein Steigungsdreieick eingezeichnet. Wie groß ist jeweils die Steigung der gegebenen Geraden? 5 G g b n Übungsblatt: LINEARE FUNKTIONEN 5A/5D sind die Geraden durch ihre Ausschnitte ihrer Graphen als auch durch ihre Gleichungen. Für jede der Geraden ist außerdem ein Steigungsdreieick eingezeichnet, allerdings fehlen in den Darstellungen die x-Achsen. Zeichne jeweils die x-Achsen passend ein! 6) Gegeben sind zwei Geraden und durch die folgenden Gleichungen: : 2x y 3 : 6 3 4 Woran erkannt man, dass und zueinander parallel sind? 7) Gegeben sind zwei Geraden und durch die folgenden Gleichungen: : 3 : 3 by c Wähle für und solche Werte, dass und keinen Punkt gemeinsam haben. Wie viele verschiedene Werte für und stehen dabei zur Auswahl? 8) Gegeben sind zwei Geraden und durch die folgenden Gleichungen: : 3 : 3 by 5 Wähle einen geeigneten Wert für , sodass und genau einen Punkt gemeinsam haben. Wie viele verschiedene Werte für stehen dabei zur Auswahl? 9) Gegeben ist die Geraden durch die folgende Gleichung: : 2 4 Auf liegen die Punkte A( A y ) und B( B y ) mit B x . Für die y-Koordinaten dieser Punkte gilt: yB y yB y yB y Die Frage lässt sich nicht beantworten, da keine konkreten Koordinaten bekannt sind. Falls du eine der drei Alternativen der ersten Zeile gewählt hast und somit glaubst, die Frage doch beantworten zu können: Begründe deine Antwort! 10) Eine Gerade ist gegeben durch 2 Punkte in einer unvollständig ausgefüllten Wertetabelle: Übungsblatt: LINEARE FUNKTIONEN 5A/5D -10 -5 0 5 10 15 20 2 8 a) Vervollständige die Wertetabelle möglichst ohne die Gleichung von zu ermitteln. b) Ermittle die Gleichung von möglichst ohne Rechnung. 11) Von fünf Funktionen kennt man jeweils einige Wertepaare: Welche der Funktionen könnten lineare Funktionen sein? Warum lautet die Frage könnten lineare Funktionen sein und nicht sind lineare Funktionen? 12) Im Ort Fußlahmhausen gibt es drei Taxiunternehmen mit unterschiedlichen Tarifen: Taxi kostet 1,25 €/km. Taxi kostet 1,15 €/km und 0,05€ für jede Minute Fahrzeit. Taxi kostet 1,00 €/km und eine Grundgebühr von 1,75€. a) Herr Faul fährt bei einer Stadtrundfahrt 6 km in 10 Minuten, Frau Bequem braucht wegen längerer Wartezeiten an Ampeln für dieselbe Strecke 13 Minuten. Welches Taxi wäre jeweils am billigsten gewesen? b) Wie weit kann man mit 25 € mit den verschiedenen Taxen kommen? Lösungen: a) 7,5/7,4 bzw. 7,55/6,57 b) 23,25 km Übungsblatt: LINEARE FUNKTIONEN 5A/5D 13) Du kannst zwischen zwei Angeboten von Handybetreibern entscheiden: Angebot „Beon: Die monatliche Grundgebühr beträgt 15€. Für eine Minute Telefonieren in alle Netze Österreichs werden 0,06€ verrechnet. Die Abrechnung erfolgt im Minutentakt (d.h. für eine angebrochene Minute wird der volle Preis für eine Minute verrechnet). Angebot „Handycom: Keine Grundgebühr! Für eine Minute Telefonieren in alle Netze Österreichs werden 0,08€ verrechnet. Für welche monatlichen Gesprächszeiten ist das Angebot „Beon bzw. das Angebot „Handycom günstiger? Lösungen: ab 751 Minuten ist das Angebot „Beon günstiger, unter 750 Minuten ist das Angebot „Handycom günstiger; Beachte: Aber auch für Gespräche, die weniger als eine Minute dauern wird der volle Preis verrechnet, also kommst du insgesamt auf weniger als 751 „volle Minuten. 14) Zur Versorgung der Futterautomaten im Zoo „Koalabär benötigt der Tierpfleger täglich 7,5 kg Tierfutter. Zwölf Tage, nachdem das Futterlager zum letzten Mal aufgefüllt wurde, befinden sich dort noch 250 kg. a) Stelle die Funktionsgleichung auf, die diesen Sachverhalt beschreibt. b) Auf welche Menge wurde das Futterlager vor zwölf Tagen aufgefüllt? c) Nach wie vielen Tagen wäre der Vorrat endgültig aufgebraucht? Lösungen: a) 7,5x 340 b) 340 kg c) 45 1/3 Tage 15) Ergänze, so dass eine lineare Funktion entsteht! a) d) 1 12 2 3 6 4 10 -1 2 -22 12 16 34 20 48 b) e) 3 5 9,75 10,2 5 11 c) f) 10 0 15 0 30 0 3 6 -3 -1 5 3 7 11 19 Übungsblatt: LINEARE FUNKTIONEN 5A/5D Lösungen: a) 8, b) -4 c) 15 d) 41 e) 8 f) 0 Übungsblatt: LINEARE FUNKTIONEN 5A/5D 16) Gerade und Formel: Welche der angegebenen Formeln ergibt graphisch eine Gerade? Begründe! 1. kx d 2. kx 2d 3. 2x 4. 2kx d 5. 2k/x 1., 2. und 3. sind richtig, weil 1. und 3. sind richtig, weil 1., 3. und 4. sind richtig, weil 4. und 5. sind richtig, weil Alle sind richtig, weil 17) Funktionsterm zuordnen: Ordne den Graphen 1-4 den richtigen Funktionstermen a) –d) zu. Begründe jeweils deine Entscheidung. 1 3 2 4 Übungsblatt: LINEARE FUNKTIONEN 5A/5D a) 2 2,5x b) 0,5 x c) 1 – 0,5x d) 3 2,5x 18) Lineare Funktion: In der Zeichnung ist eine lineare Funktion dargestellt. a) Kennzeichne die Größen und d, lies ihren Wert ab und gib die Gleichung der linearen Funktion an. . d Gleichung der linearen Funktion: b) Kreuze die richtigen Aussagen an: Je größer die Steigung, umso steiler verläuft die Gerade. Je größer die Steigung, umso flacher verläuft die Gerade. Die Steigung ist der Quotient von Höhenunterschied zur waagrechten Entfernung. Die Steigung ist der Quotient von waagrechter Entfernung zum Höhenunterschied. In der Gleichung einer linearen Funktion wird mit der x– Achsenabschnitt bezeichnet. In der Gleichung einer linearen Funktion wird mit der y– Achsenabschnitt bezeichnet 19) Spezielle lineare Funktionen: Das Schaubild einer linearen Funktion ist eine Gerade. Wie verläuft eine Gerade, wenn in der Funktionsgleichung a) 0 b) 0 ist? Übungsblatt: LINEARE FUNKTIONEN 5A/5D Skizziere jeweils eine Gerade für Teil a) bzw. Teil b): 20) Parallele Geraden: Funktionsgleichungen Parallele Geraden erkennt man daran, dass ihre . Gegeben sind vier Geradengleichungen: g1: –3x – 5 g2: 2y –6x – 5 Kreuze die richtigen Aussagen an: g1 g3 g2 g4 g3: 5y –15x 30 g1 g2 g4: 2y 6x 10 g1 g4 21) Die Normale a) Lies die Funktionsgleichung der abgebildeten Funktion ab. b) Beantworte grafisch und rechnerisch die beiden Fragen f(-2) ? und f(x) -2, ?. c) Ermittle rechnerisch die Gleichung jener Geraden g, die zur Geraden normal ist und durch den Koordinatenursprung geht. Übungsblatt: LINEARE FUNKTIONEN 5A/5D 22) und zuordnen: a) Gib für die dargestellten linearen Funktionen an, welche Bedingungen für die Übungsblatt: LINEARE FUNKTIONEN 5A/5D Parameter und jeweils gelten müssen (Füge ein: , , ) g1: k0 d0 g2: k0 d0 g3: k0 d0 g4: k0 d0 b) Entscheide, welche der oben dargestellten Funktionen die nachfolgende reale Situation abbildet und gib die Bedeutung von und in diesem Zusammenhang an: Ein voller Tanklastwagen wird entladen. Pro Sekunde wird immer dieselbe Menge an Öl abgelassen. 23) Schnittpunkt: Gegeben sind die Gleichungen: 2y – 4 II 4y – 3x 7 a) Ermittle die Lage der Geraden und den Schnittpunkt. b) Fertige eine Zeichnung an. c) Ändere die Gerade II so, dass sie parallel zur Geraden II ist und sie die Gerade im Punkt P(3/ 3,5) schneidet. d) Wo schneiden die Geraden die y-Achse und wie kann man diesen Wert aus der Angabe ablesen?