Arbeitsblatt: Teilbarkeitsregeln

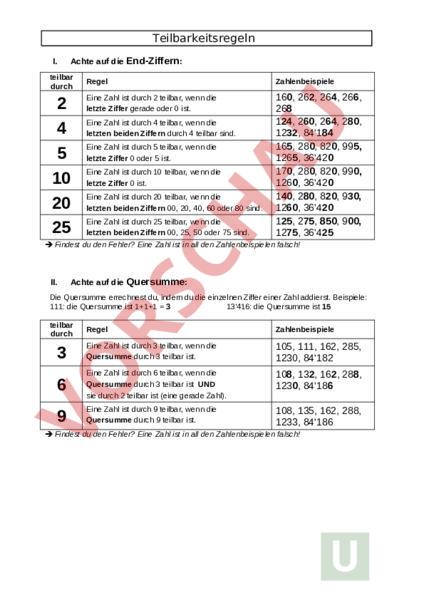
Teilbarkeitsregeln I. Achte auf die End-Ziffern: teilbar durch 2 4 5 10 20 25 Regel Zahlenbeispiele Eine Zahl ist durch 2 teilbar, wenn die letzte Ziffer gerade oder 0 ist. 160, 262, 264, 266, 268 124, 260, 264, 280, 1232, 84184 165, 280, 820, 995, 1265, 36420 170, 280, 820, 990, 1260, 36420 140, 280, 820, 930, 1260, 36420 125, 275, 850, 900, 1275, 36425 Eine Zahl ist durch 4 teilbar, wenn die letzten beiden Ziffern durch 4 teilbar sind. Eine Zahl ist durch 5 teilbar, wenn die letzte Ziffer 0 oder 5 ist. Eine Zahl ist durch 10 teilbar, wenn die letzte Ziffer 0 ist. Eine Zahl ist durch 20 teilbar, wenn die letzten beiden Ziffern 00, 20, 40, 60 oder 80 sind. Eine Zahl ist durch 25 teilbar, wenn die letzten beiden Ziffern 00, 25, 50 oder 75 sind. Findest du den Fehler? Eine Zahl ist in all den Zahlenbeispielen falsch! II. Achte auf die Quersumme: Die Quersumme errechnest du, indem du die einzelnen Ziffer einer Zahl addierst. Beispiele: 111: die Quersumme ist 111 3 13416: die Quersumme ist 15 teilbar durch Regel Zahlenbeispiele 3 Eine Zahl ist durch 3 teilbar, wenn die Quersumme durch 3 teilbar ist. 105, 111, 162, 285, 1230, 84182 6 Eine Zahl ist durch 6 teilbar, wenn die Quersumme durch 3 teilbar ist UND sie durch 2 teilbar ist (eine gerade Zahl). 108, 132, 162, 288, 1230, 84186 9 Eine Zahl ist durch 9 teilbar, wenn die Quersumme durch 9 teilbar ist. 108, 135, 162, 288, 1233, 84186 Findest du den Fehler? Eine Zahl ist in all den Zahlenbeispielen falsch! Arbeitsblatt Teilbarkeit teilbar durch Name: Welche Zahlen von 50 bis 150 musst du hier einschreiben? 2 3 4 5 6 9 10 20 25 1. Welche Zahlen zwischen 50 und 150 kommen in dieser Liste nicht vor? 2. Streiche jetzt oben noch die Zahlen, von denen du weisst, dass sie auch nicht durch die andern Teiler teilbar sind (7, 8, 11, 13, etc.) Die übrig bleibenden sind PRIMZAHLEN. Lösungen: