Arbeitsblatt: Masstheorie - Nicht messbare Grössen

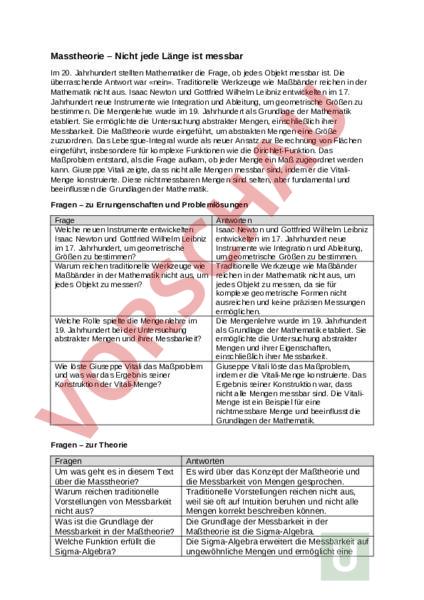
Masstheorie – Nicht jede Länge ist messbar Im 20. Jahrhundert stellten Mathematiker die Frage, ob jedes Objekt messbar ist. Die überraschende Antwort war «nein». Traditionelle Werkzeuge wie Maßbänder reichen in der Mathematik nicht aus. Isaac Newton und Gottfried Wilhelm Leibniz entwickelten im 17. Jahrhundert neue Instrumente wie Integration und Ableitung, um geometrische Größen zu bestimmen. Die Mengenlehre wurde im 19. Jahrhundert als Grundlage der Mathematik etabliert. Sie ermöglichte die Untersuchung abstrakter Mengen, einschließlich ihrer Messbarkeit. Die Maßtheorie wurde eingeführt, um abstrakten Mengen eine Größe zuzuordnen. Das Lebesgue-Integral wurde als neuer Ansatz zur Berechnung von Flächen eingeführt, insbesondere für komplexe Funktionen wie die Dirichlet-Funktion. Das Maßproblem entstand, als die Frage aufkam, ob jeder Menge ein Maß zugeordnet werden kann. Giuseppe Vitali zeigte, dass nicht alle Mengen messbar sind, indem er die VitaliMenge konstruierte. Diese nichtmessbaren Mengen sind selten, aber fundamental und beeinflussen die Grundlagen der Mathematik. Fragen – zu Errungenschaften und Problemlösungen Frage Welche neuen Instrumente entwickelten Isaac Newton und Gottfried Wilhelm Leibniz im 17. Jahrhundert, um geometrische Größen zu bestimmen? Warum reichen traditionelle Werkzeuge wie Maßbänder in der Mathematik nicht aus, um jedes Objekt zu messen? Welche Rolle spielte die Mengenlehre im 19. Jahrhundert bei der Untersuchung abstrakter Mengen und ihrer Messbarkeit? Wie löste Giuseppe Vitali das Maßproblem und was war das Ergebnis seiner Konstruktion der Vitali-Menge? Antworten Isaac Newton und Gottfried Wilhelm Leibniz entwickelten im 17. Jahrhundert neue Instrumente wie Integration und Ableitung, um geometrische Größen zu bestimmen. Traditionelle Werkzeuge wie Maßbänder reichen in der Mathematik nicht aus, um jedes Objekt zu messen, da sie für komplexe geometrische Formen nicht ausreichen und keine präzisen Messungen ermöglichen. Die Mengenlehre wurde im 19. Jahrhundert als Grundlage der Mathematik etabliert. Sie ermöglichte die Untersuchung abstrakter Mengen und ihrer Eigenschaften, einschließlich ihrer Messbarkeit. Giuseppe Vitali löste das Maßproblem, indem er die Vitali-Menge konstruierte. Das Ergebnis seiner Konstruktion war, dass nicht alle Mengen messbar sind. Die VitaliMenge ist ein Beispiel für eine nichtmessbare Menge und beeinflusst die Grundlagen der Mathematik. Fragen – zur Theorie Fragen Um was geht es in diesem Text über die Masstheorie? Warum reichen traditionelle Vorstellungen von Messbarkeit nicht aus? Was ist die Grundlage der Messbarkeit in der Maßtheorie? Welche Funktion erfüllt die Sigma-Algebra? Antworten Es wird über das Konzept der Maßtheorie und die Messbarkeit von Mengen gesprochen. Traditionelle Vorstellungen reichen nicht aus, weil sie oft auf Intuition beruhen und nicht alle Mengen korrekt beschreiben können. Die Grundlage der Messbarkeit in der Maßtheorie ist die Sigma-Algebra. Die Sigma-Algebra erweitert die Messbarkeit auf ungewöhnliche Mengen und ermöglicht eine Warum ist die Maßtheorie wichtig? Wie unterscheidet sich die Maßtheorie von herkömmlichen Vorstellungen? Welche Rolle spielt die formale Definition in der Maßtheorie? Was sind Beispiele für ungewöhnliche Mengen, die mit Hilfe der Maßtheorie gemessen werden können? Wie beeinflusst die Maßtheorie unser Verständnis von Messbarkeit? Warum ist die Erweiterung der traditionellen Vorstellungen von Messbarkeit notwendig? formale Definition der Messbarkeit. Die Maßtheorie ist wichtig, um eine präzise Definition von Messbarkeit bereitzustellen und ungewöhnliche Mengen zu analysieren. Die Maßtheorie unterscheidet sich von herkömmlichen Vorstellungen, indem sie eine formale Definition der Messbarkeit bietet und auch ungewöhnliche Mengen berücksichtigt. Die formale Definition in der Maßtheorie ist entscheidend, um Messbarkeit genau zu definieren und zu analysieren. Beispiele für ungewöhnliche Mengen, die mit Hilfe der Maßtheorie gemessen werden können, sind Fraktale oder nicht-leere Mengen ohne Längenmaß. Die Maßtheorie erweitert unser Verständnis von Messbarkeit, indem sie eine präzise und formale Definition bereitstellt. Die Erweiterung der traditionellen Vorstellungen von Messbarkeit ist notwendig, um auch ungewöhnliche Mengen korrekt zu analysieren und zu messen.