Arbeitsblatt: Test Proportionalität

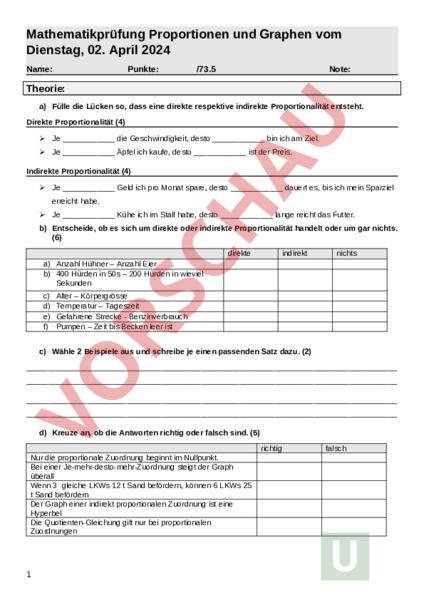
Mathematikprüfung Proportionen und Graphen vom Dienstag, 02. April 2024 Name: Punkte: /73.5 Note: Theorie: a) Fülle die Lücken so, dass eine direkte respektive indirekte Proportionalität entsteht. Direkte Proportionalität (4) Je die Geschwindigkeit, desto bin ich am Ziel. Je Äpfel ich kaufe, desto ist der Preis. Indirekte Proportionalität (4) Je Geld ich pro Monat spare, desto dauert es, bis ich mein Sparziel erreicht habe. Je Kühe ich im Stall habe, desto lange reicht das Futter. b) Entscheide, ob es sich um direkte oder indirekte Proportionalität handelt oder um gar nichts. (6) direkte indirekt nichts a) Anzahl Hühner – Anzahl Eier b) 400 Hürden in 50s – 200 Hürden in wieviel Sekunden c) d) e) f) Alter – Körpergrösse Temperatur – Tageszeit Gefahrene Strecke Benzinverbrauch Pumpen – Zeit bis Becken leer ist c) Wähle 2 Beispiele aus und schreibe je einen passenden Satz dazu. (2) d) Kreuze an, ob die Antworten richtig oder falsch sind. (5) richtig Nur die proportionale Zuordnung beginnt im Nullpunkt. Bei einer Je-mehr-desto-mehr-Zuordnung steigt der Graph überall Wenn 3 gleiche LKWs 12 Sand befördern, können 6 LKWs 25 Sand befördern Der Graph einer indirekt proportionalen Zuordnung ist eine Hyperbel Die Quotienten-Gleichung gilt nur bei proportionalen Zuordnungen 1 falsch Proportionale Umgekehrt Proportionale Zuordnung: a) Berechne die fehlenden Werte der direkten Zuordnungen. (8) b) Der Heuvorrat eines Reitstalls reicht bei 8 Pferden für 30 Tage. Wie lange reicht er, wenn sich die Anzahl der Pferde auf 15 bzw. 20 erhöht? (2) Wertetabelle: Ergänze die Angaben um zwei weitere passende Wertepaare und fülle die Wertetabelle aus. (3) 8 15 20 30 Graphen: Lege ein Koordinatensystem an und zeichne einen Graphen für diese Wertetabelle. (4) Handelt es sich hier um eine direkte oder um eine indirekte Proportion? (1) 2 Berechne folgende proportionalen Zuordnungen mit Hilfe eines Dreisatzes oder mit einer anderen Methode. Die Ausrechnung muss klar ersichtlich sein. a) Wie viel Benzin bezahlt Frau Meier für 25 Liter Benzin, wenn Herr Kessler für 35 Liter 57.60.bezahlt? Runde auf 5 Rappen genau. (2) b) Wie oft dreht sich ein Rad in 40 Sekunden, wenn es sich in 15 Sekunden 6-mal dreht? (2) c) Ein Velofahrer misst nach 3,5 Km Fahrt in der Ebene eine Zwischenzeit von 25 Minuten. Berechne seine Geschwindigkeit in Km h. (2) d) Ein Dreieck hat den Flächeninhalt 50 cm. Beschreibe die Beziehung zwischen der Grundseite und der Höhe in einer Gleichung (Formel). Belege diesen Zusammenhang mit mindestens zwei selbst gewählten Wertepaaren. (4) 50 . (). , . 3 e) Handelt es sich bei diesen Graphen um eine proportionale (p) oder umgekehrt proportionale (up) Zuordnung oder weder noch (x)? Schreibe in die Kästchen. (3) Umgekehrt proportionale Zuordnung: a) Kreuze die richtige(n) Antwort(en) an. (1) Man erkennt eine umgekehrt proportionale Zuordnung daran, dass. die Summe der Grössen immer gleich bleibt. Richtig die Differenz der Grössen immer gleich bleibt. das Produkt der Grössen immer gleich bleibt. der Quotient der Grössen immer gleich bleibt. b) Ist diese Zuordnung proportional oder nicht? Begründe deine Antwort mit einer Ausrechnung. (2) 4 c) Berechne: (2) d) 27 Personen bauen einen Weg in 38 Stunden. Wie viele Personen braucht es zusätzlich, um in 9 Stunden fertig zu sein? Zeige deine Ausrechnungen. (3) e) 3 Maschinen produzieren in einer Stunde 45 Werkstücke. Wie lange würde die Produktion der 45 Werkstücke dauern, wenn dafür 8 Maschinen zu Verfügung stehen? (2) f) Die in der Tabelle dargestellte Zuordnung ist antiproportional. Vervollständige die Tabelle. (3.5) 1 2 5 250 5 10 100 20 50 100 Füllhöhen: a) Welches Gefäss gehört zu welchem Graphen? (6) b) Welche Gefässe bleiben übrig? Zeichne für die übriggebliebenen Gefässe je einen passenden Graphen. (2) 6