Arbeitsblatt: angepasste Lernkontrolle Tabellen untersuchen, Teiler, Vielfache , Primzahlen, Quadratzahlen

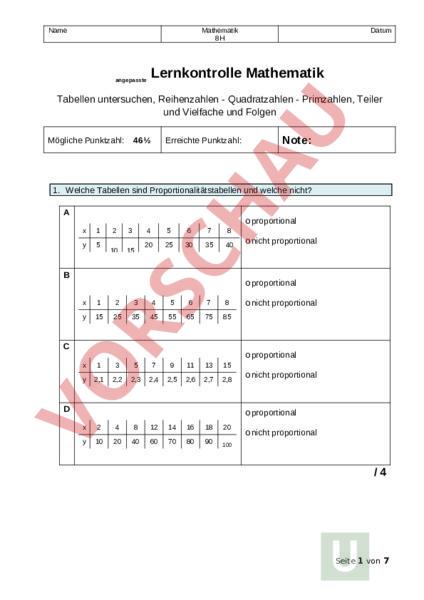
Name Mathematik 8H Datum Lernkontrolle Mathematik angepasste Tabellen untersuchen, Reihenzahlen Quadratzahlen Primzahlen, Teiler und Vielfache und Folgen Mögliche Punktzahl: 46 Erreichte Punktzahl: Note: 1. Welche Tabellen sind Proportionalitätstabellen und welche nicht? oproportional 1 5 2 3 10 15 4 5 6 7 8 20 25 30 35 40 onicht proportional oproportional 1 2 3 4 5 6 7 8 15 25 35 45 55 65 75 85 1 3 5 7 9 11 13 15 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 onicht proportional oproportional onicht proportional oproportional 2 4 8 12 14 16 18 20 10 20 40 60 70 80 90 100 onicht proportional /4 Seite 1 von 7 2. Ergänze die zwei Tabellen. Welche sind Proportionalitätstabellen? Eine Briefmarke für einen Standard-A-Post-Brief kostet 1.20 Fr. Anzahl Briefmarken 1 2 4 5 10 20 40 100 Kosten [Fr.] Das ist eine Proportionalitätstabelle. Das ist keine Proportionalitätstabelle. 1 Liter Benzin kostet an der Tankstelle 1.50 Fr. Anzahl Liter 1 2 5 10 20 25 30 40 Preis [Fr.] Das ist eine Proportionalitätstabelle. Das ist keine Proportionalitätstabelle. Mirko sagt eine Zahl. Judith sagt darauf eine Zahl, die jeweils um 5 grösser ist. Mirko sagt: 1 3 5 10 15 Judith sagt: 50 95 100 100 Das ist eine Proportionalitätstabelle. Das ist keine Proportionalitätstabelle /6 3. Markiere im Hunderterfeld alle Quadratzahlen bis 100! 4.5 Seite 2 von 7 4. Berechne die folgenden Quadratzahlen. Du kannst schriftlich rechnen! 13 13 /2 18 18 5. In der Hundertertafel gibt es in einer Spalte helle Zahlen. Wie heissen die hellen Zahlen in der Hundertertafel? Diese Zahlen haben in der Einerstelle eine 3. Kannst du erklären, was diese Zahlen noch gemeinsam haben? /2 6. Ergänze die Tabelle. Setze für jeweils die roten Zahlen ein und für die blauen Zahlen! Kreise alle Primzahlen in den grauen Spalten mit rot ein wie im Beispiel 4 5 5 6 6 7 7 8 4x5 Spalte Spalte II Spalte III axb axb1 axb–1 20 4x51 21 4x5-1 /4 19 Seite 3 von 7 7. Bestimme alle Teiler von T36 T42 /2 8. Bestimme wie im Beispiel die Vielfachen! Achtung gehe nicht weiter als 150! Zahl 18 21 35 Vielfache 18, 36, 54, 72, 90, 108, 126, 144 /2 9. 102, 134, 308, 321, 510, 735, 870, 1200, Welche dieser Zahlen sind durch 2 teilbar? Welche dieser Zahlen sind durch 3 teilbar? (Tipp: Bilde die Quersumme) Welche dieser Zahlen sind durch 10 teilbar? /3 10. Welches ist jeweils der grösste gemeinsame Teiler (ggT) des Zahlenpaars? 24 48 ggT /3 Seite 4 von 7 11. Welches ist jeweils das kleinste gemeinsame Vielfache (kgV) des Zahlenpaars? V11 V13 kgV /3 12. Zeichne für die Folgen 1 bis 3 jeweils die Figur 5 und fülle unten die Tabelle richtig aus! Folge 1 Anzahl Quadrate Folge 2 Anzahl Hölzchen Folge 3 Anzahl Würfel Figur 1 Figur 2 Figur 3 Figur 4 Figur 5 Figur 6 Figur 10 5 6 1 Seite 5 von 7 /7 Wie fühlst du dich am Ende der Lernkontrolle? Kreuze an. Seite 6 von 7 Seite 7 von 7