Arbeitsblatt: Tangens am Einheitskreis

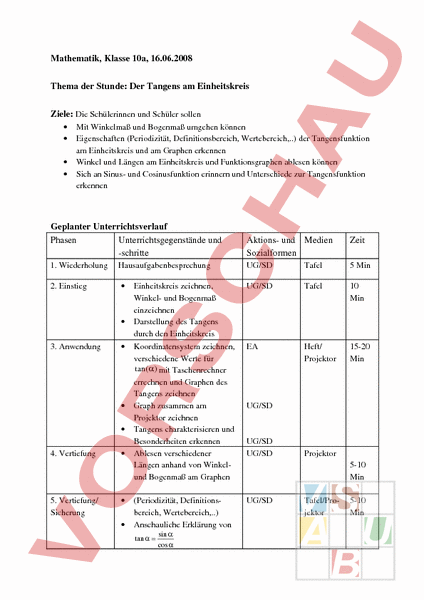
Mathematik, Klasse 10a, 16.06.2008 Thema der Stunde: Der Tangens am Einheitskreis Ziele: Die Schülerinnen und Schüler sollen • • • • Mit Winkelmaß und Bogenmaß umgehen können Eigenschaften (Periodizität, Definitionsbereich, Wertebereich,) der Tangensfunktion am Einheitskreis und am Graphen erkennen Winkel und Längen am Einheitskreis und Funktionsgraphen ablesen können Sich an Sinus und Cosinusfunktion erinnern und Unterschiede zur Tangensfunktion erkennen Geplanter Unterrichtsverlauf Phasen Unterrichtsgegenstände und schritte Aktions und Medien Sozialformen Zeit 1. Wiederholung Hausaufgabenbesprechung UG/SD Tafel 5 Min 2. Einstieg • Einheitskreis zeichnen, Winkel und Bogenmaß einzeichnen Darstellung des Tangens durch den Einheitskreis UG/SD Tafel 10 Min Koordinatensystem zeichnen, verschiedene Werte für tan() mit Taschenrechner errechnen und Graphen des Tangens zeichnen Graph zusammen am Projektor zeichnen Tangens charakterisieren und Besonderheiten erkennen Ablesen verschiedener Längen anhand von Winkel und Bogenmaß am Graphen EA Heft/ Projektor 1520 Min (Periodizität, Definitions bereich, Wertebereich,) Anschauliche Erklärung von UG/SD • 3. Anwendung • • • 4. Vertiefung • 5. Vertiefung/ Sicherung • • tan sin cos UG/SD UG/SD UG/SD Projektor Tafel/Pro jektor 510 Min 510 Min • Eigenschaften: Sinus, Cosinus und Tangensgraph UG: Unterrichtsgespräch, SD: Schülerdarbietung, EA: Einzelarbeit, LD: Lehrerdarbietung Wiederholung: SinusFunktion Eigenschaften: Definitionsbereich: von –unendlich bis unendlich Wertebereich: zwischen 1 und 1 Periodizität: 360 CosinusSinus um 90 nach rechts verschoben Nullstellen bei 180a Cosinus: Nullstellen bei 90a Unterschiede:Tangens: Definitionsbereich nicht definiert für 90180a für ganzes Tangens: keine Begrenzung des Wertebereiches Thema: Tangensfunktion Erinnerung: tan() Gegenkathete Ankathete An der Tafel: Jemand zeichnet einen Einheitskreis und jeder im Heft mit r10cm Frage: Kann man ein rechtwinkliges Dreieck einzeichnen, sodass die Eigenschaften des Tangens ablesbar sind? Einheitskreis mit Bogenmaß und Winkelmaß beschriften tan(30) 0,5773 0,58 Wie groß sind tan(45) 1 tan(60) 1, 732 1, 73 Zeichne Koordinatensystem mit Maßeinheit 0,5cm10 auf der xAchse von 180280 Quer im Heft! Mit Taschenrechner verschiedene Längen der Gegenkathete bei unterschiedlichen Winkeln errechnen. tan(180) 0 tan(30 0,57735 tan(150) 0,57735 tan(45 1 tan(130) 1,191753 tan(65 2,1445 tan(100) 5, 67128 tan(75 3,73205 tan(60) 1, 73205 tan(80) 5,67128 tan(40) 0,83909 tan(85) 11, 4300 tan(135) 1 tan(150) 0,57735 tan(165) 0, 26795 tan(180) 0 tan(190) 0,17632 tan(200) 0,3639 tan(225) 1 tan(15) 0, 26795 tan(100 5,67128 tan(230) 1,19175 tan(0) 0 tan(105 3,73205 tan(260) 5, 67128 tan(15) 0, 26795 tan(120 1,73205 tan(280) 5, 67128 Trage die Längen in das Bild ein, jeder bei sich und dann vorne am Projektor Warum ergibt tan(90)Error? Nicht definiert, kein Dreieck einzeichenbar! nun bildlich am Graphen des Tangens, nicht definiert, da Graph gegen 90 gegen und unendlich geht sin 90, ,sogar (2k 1) nicht definiert (Definitionsbereich) cos 2 2 tan() tan( n), ¢ Periodizität, was ist das?: 180 tan() tan(150)tan(30)tan(210)tan(390)tan(570). Verschiedene Werte am Graphen ablesen, ohne Taschenrechner: tan(25) tan(335) tan(155) 0, 466 tan(2) tan(360) 0 tan(360 180) tan( tan(30) 0,577 tan(210) 6 3 tan( tan(270) tan(270 180) tan(90) nichtdef 2 3 tan( tan(135) 1 tan(315) 4 5 tan( tan(225) 1 tan(45) 4 2 tan( tan(40) 0,84 tan(220) 9 9 tan( tan(90) nichtdef 2 tan(345) tan(345 180) tan(165) 0, 2679 tan(5) tan(180) 0 Tangens Periodizität: bei 180, also tan() tan( n), ¢ Definitionsbereich nicht definiert für 90180a für ganzes Wertebereich: keine Begrenzung